[AI & ML Introduction] Maximum Likelihood Estimation (MLE)

Thumbtack Question

---

압정을 던져서 앞면과 뒷면을 결정하는 도박을 하고 있다고 가정해보겠습니다. 과학적인 의사결정을 하는 엔지니어라면 앞, 뒤 중 어디에 돈을 거는 것이 합리적일까요? 도박에 합리적인 선택이 있을 리 만무하지만, 그러한 내용은 잠시 접어두도록 하겠습니다. 합리적인 의사결정을 위해서는 어떤 행동을 해야 할까요? 

 

Fig. 1 압정을 던지면 어떤 결과를 얻을까?

 

아마 엔지니어는 압정을 먼저 던져볼 것입니다. 압정을 5번 던져서 앞면이 3번, 뒷면이 2번 나왔다고 가정해 보겠습니다. 그렇다면 엔지니어는 압정의 앞면이 나올 확률이 $\frac{3}{5}$, 뒷면이 나올 확률이 $\frac{2}{5}$라고 말할 수 있을 것입니다. 그렇다면 그 확률은 어떻게 정의된 것일까요? 던지는 것과 확률은 어떤 상관이 있을까요?

 

Binomial Distribution

---

이항 분포(Binomial Distribution)는 연속된 n번의 독립적 시행해서 각 시행의 성공 확률이 $\theta$ 일때의 이산 확률 분포(Discrete Probability Distribution)라고 정의할 수 있습니다. 압정을 던지는 행위는 서로 독립인 사건이며 동일한 이항 분포를 따릅니다(iid: independent and identically distributed). 즉, 압정을 던지는 확률을 다음과 같이 표현할 수 있습니다. (여기서 H는 압정의 앞면, T는 뒷면으로 정의한다.)

 

확률을 이항 분포로 표현하기 위해서 다음과 같은 변수를 정의할 수 있습니다.

 

n과 p 값이 주어졌을 때, 앞면의 압정이 k개만큼 나올 확률은 다음과 같이 구할 수 있습니다.

 

그렇지만 우리는 $\theta$ 값을 모르기에 이 수식을 지금 당장 활용할 수는 없습니다. 그렇기에 약간 관점을 바꾸어 보려고 합니다. $\theta$라는 값이 주어졌을 때, D라는 데이터가 관측될 확률은 Eqn.1 과 같이 정의됩니다. ($\because$ iid)

 

 

Maximum Likelihood Estimation

---

여기서 한 가지 짚고 넘어갈 점은 엔지니어는 압정의 도박 결과(=데이터 D)가 이항 분포를 따른다는 가정을 하고 있습니다. H와 T의 이항 분포로 표현하였지만 사실은 이항 분포 보다도 압정의 결과를 더 잘 규명해 줄 수 있는 분포가 분명 존재할 가능성이 있습니다! 그렇기에 데이터를 규명하기에 앞서 분기점이 발생하게 됩니다. 첫 번째는 압정의 데이터를 가장 잘 반영할 수 있는 분포를 직접 찾아내는 것이고, 두 번째는 이항 분포를 따른다는 가정에 힘을 실어주기 위해 가장 최적의 $\theta$를 찾아내는 방법입니다. 첫 번째는 논외로 하고, 두 번째 방법에 포커스를 맞춰보겠습니다. 이항 분포에서 데이터 D가 나올 가능성이 가장 높은 $\theta$를 찾는 것입니다. 이렇게 $\theta$를 찾는 방법을 최대 우도 추정(Maximum Likelihood Estimation)이라고 하며 식은 Eqn.2 와 같습니다.

 

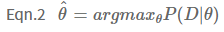
식은 간단합니다. 관측된 데이터 D를 $\theta$에 관한 함수로 보고 데이터 D가 관측될 수 있는 정도를 최대화하는 $\theta$를 구할 것이고, 그것을 $\hat{\theta}$이라고 한다는 의미입니다. 이제 MLE 계산을 위해서 식을 살짝 바꾸어 보겠습니다.

 

$\hat{\theta}$를 구하기 위해서는 데이터를 가장 잘 설명하는 $\theta$를 찾아야 합니다. 여기서 계산의 편의성을 위해서 ln 함수를 씌워서 계산하겠습니다. 일반적으로 최대화 문제를 풀 때는 미분해서 0이 되는 해를 구하면 되는데, 바로 미분하기 어려울 때 ln를 취하면 미분이 쉬워지는 케이스입니다. (ln 함수가 증가함수 이기 때문에, f가 최대가 되는 점에서는 log(f)도 최대가 되는 원리입니다.)

 

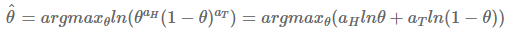
값을 미분해서 0이 되는 지점을 찾으면 데이터 D가 나올 정도를 최대화하는 $\theta$를 구할 수 있습니다.

 

여기서 구한 $\theta$ 식을 보면 느낌이 바로 오지 않나요? $a_{H}$와 $a_{T}$에 값을 대입해 본다면 압정의 앞면이 나올 확률이 $\frac{3}{5}$가 됨을 MLE를 통해 증명하였습니다! 하지만 여기서 멈출 수는 없습니다.

Hoeffding's Inequality

---

MLE를 통해서 데이터 기반의 확률을 구해보았습니다. 여기서 한 가지, 만약 5번의 시행을 한 것이 아니라 50번의 시행을 했고 그중에서 앞 면이 30번 뒷 면이 20번 나왔다고 가정해보겠습니다. MLE로 구한 식에 해당 값을 대입하면 압정을 던졌을 때 앞면이 나올 확률은 0.6입니다.  그렇다면 시행을 많이 하는 것이 아무런 도움이 되지 않을까요? 꼭 그렇지는 않습니다.

 

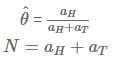
새로운 $\theta^*$을 정의하겠습니다. $\theta^*$는 아무런 에러가 없는, 즉 압정을 던져서 앞면이 나올 정확한 확률 값입니다. 그렇다면 MLE로 추론한 $\hat{\theta}$와 참인 파리미터 $\theta^*$의 차이가 특정 오차 범위(Error bound $\epsilon$)보다 클 확률을 규명하는 호프딩의 부등식(Hoeffding's Inequality)을 적용해 볼 수 있습니다.

 

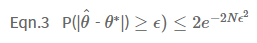
여기서 N이 시행 횟수입니다. 만약 오차 범위인 입실론의 값이 커지면, 우변이 작아짐으로 추정한 파라미터와 참인 파라미터의 값 차이가 오차 범위 이상으로 발생할 확률은 낮아집니다. 만약 여기서 시행 횟수인 N이 커지면 어떻게 될까요? 우변이 작아짐으로, 역시 오차 범위 이상의 값 차이를 가질 확률은 낮아지게 됩니다. 호프딩의 부등식을 활용하면 시행 횟수 N을 키우는 일이 얼마나 유용한 행위인지를 알 수 있습니다. N을 키움으로서 파라미터 값에 0.1이라는 오차가 발생할 확률이 0.01% 보다 작을 확률도 구해볼 수 있게 됩니다.

 

이러한 접근 법을 PAC (Probably Approximately Correct) learning이라고 합니다. PAC Learning이란 수학적으로 머신러닝 모델을 분석하는 프레임워크으로, "높은 확률로 주어진 모델이 작은 에러를 가진다(Approximatly Correct)"와 같은 식의 분석을 할 수 있는 방법입니다. 데이터에 전혀 노이즈가 없다고 하더라도 정확하게 에러가 0이 되는 모델을 얻는 것은 거의 불가능하기 때문에 확률적으로, 그리고 에러라는 관점에서 모델을 분석하는 접근법입니다.