[Calculus] Taylor Series (테일러 급수)

테일러 급수란?

---

 테일러 급수(Taylor Series)는 알려지지 않은 어떤 함수 f(x)를 다항식들의 합으로 표현하는 것을 의미합니다. 머신러닝을 공부하다 보면 파라미터의 최적화 과정에서 테일러 급수가 종종 사용됩니다. 간단하게 개념을 정리하고 예시를 통해 테일러 급수를 어떻게 활용할 수 있을지에 대한 시야를 넓혀보고자 합니다. Eqn.1은 테일러 급수로 함수를 나타내는 방법으로 테일러 전개(Taylor Expansion)를 의미합니다. 이때, 함수 f(x)에 대한 다항함수를 a에서 f(x)의 테일러 급수라 하며, a=0인 테일러 급수는 맥클로린 급수(Meclaurin Series)라고 합니다.

 

Eqn. 1. Taylor Expansion

 

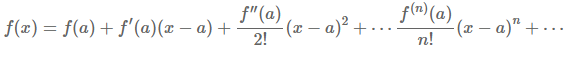
테일러 전개의 구성

---

 테일러 전개는 함수를 수열로 변환합니다. 즉, 함수의 문제를 Eqn. 2처럼 수열의 문제로 바꾸어 줍니다. 함수값을 구하기 힘들 때 그 값을 수열의 연산을 통해서 구함으로서 문제를 쉽게 해결할 수 있게 됩니다. 그렇기에 Eqn. 1의 식의 구성에 대해서 간단하게 짚고 넘어가고자 합니다. Eqn.1의 테일러 전개의 계수 a는 a를 중심으로 테일러 전개를 한다는 의미로, 주어진 f(x)에 대해 x=a인 지점에서 계속하여 미분을 수행하게 됩니다. 심플함을 위해서 x=0을 중심으로 테일러 급수를 전개하면 아래와 같습니다. 여기서 x에 0을 대입하면, $a_{0}$이 f(0)이라는 것을 알게 됩니다. 즉, 주어진 함수에 0을 대입한 값이 테일러 전개의 첫 번째 계수가 됩니다.

 

Eqn. 2. Transform Function f(x) to Taylor Series

 

 이제 테일러 전개의 상수항인 $a_{n}$를 구해보겠습니다. $a_{1}$을 구하기 위해서는 $a_{0}$ 부분을 제거해야 합니다. 하지만 복잡한 계산은 필요 없습니다. 아래와 같이 간단하게 함수 f(x)를 x에 대해 미분을 하면 $a_{1}$을 쉽게 계산할 수 있습니다.

 

 

 그다음으로 $a_{2}$를 구해보겠습니다. 역시 f(x)를 두 번 미분하면 쉽게 구할 수 있습니다.

 

 

 x에 대해서 미분을 하면 계수가 내려오기에 $a_{n}$ 앞에는 n! 가 붙게 됨을 확인할 수 있습니다. 즉, 다음과 같은 식이 성립합니다.

 

 

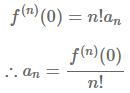
 위 식을 대입하면, 테일러 전개의 식을 구할 수 있습니다.

 

Example

 

---

 테일러 급수가 무엇인지, 테일러 전개는 어떻게 구성되는지를 알아보았습니다. 그렇다면 어떤 상황에서 테일러 급수를 어떻게 적용하는지 간단한 예제를 들어보겠습니다. 테일러 전개는 미분을 사용하기 때문에, 주어진 함수 f(x)는 무한 번 미분 가능해야 합니다. 단, 테일러 급수는 f(x)에 수렴하게 됨으로 미분계수가 0이라도 상관은 없습니다. exp x는 example을 위한 함수입니다.

 

 

 테일러 전개는 함수 값을 수열로 만들어 주며, 수열의 값은 함수 값에 근사하게 됩니다. 테일러 전개의 구성 부분에서 했던 방법과 동일하게 수열의 일반항을 구하고, 함수 값의 근사치를 구해보겠습니다. $e^x$는 미분해도 그 형태가 변하지 않는 특성을 가지고 있고, 0을 대입하면 값이 1이 됨으로 테일러 전개의 상수항 $a_{i}$를 구하는 방법은 역시 간단합니다. 먼저 함수를 수열로 바꾸기 위해 기본 식을 가정합니다.

 

 

 우리는 여기서 테일러 급수의 상수항 $a_{k}$의 형태를 알고 있습니다.

 

 

 주어진 함수 $e^x$는 미분해도 그 형태가 동일하고, x에 0을 대입하면 그 값은 1이 됨으로 $a_{k}$의 $f^{(k)}(0)$ 항은 모두 제거되고, k! 부분은 남아서 테일러 급수의 상수항 형태를 만듭니다. 그렇기에 테일러 전개는 다음과 같은 형태를 가지게 됩니다.

 

 

 이제 함수 값을 테일러 전개를 통해 구해보겠습니다. x=1일때, 함수 값을 통해 e의 값을 구하는 방법은 다음과 같고, 함수값을 소수점 15자리 까지 계산해 보면 2.718281828459045 입니다.

 

 

 함수 값을 직접 계산하지 않고 테일러 급수를 통해 근사시키면 어떨까요? 간단한 python 코드를 통해 테일러 전개의 k 값이 커질수록 원래 값과의 오차가 얼마나 되는지 보이면 다음과 같습니다.

 

Python Code

 

Output

 

 간단한 코드임으로 굳이 리뷰를 하지 않겠습니다. 결과값을 보면 18번째 반복 부터는 소수점 15자리 이하의 오차가 발생함을 확인할 수 있습니다. 즉, 테일러 급수를 통해서 함수값을 근사적으로 구한 것입니다! 여기까지 계산하기 어려운 함수의 값을 수열 연산을 통해 구하는 테일러 급수에 관한 설명이었습니다.